导数定义
对于某个函数,图像上有两个点A和B,当B点离A点越来越近的时候,直线AB的斜率越来越接近与A点函数的切线。
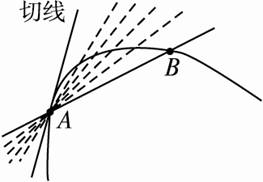
使用代数表示,可以得到AB直线的斜率为:
$$K_{AB}=\frac{f(x_{B})-f(x_{A})}{x_{B}-x_{A}}$$
Tips:斜率公式可以根据\(\left\{\begin{matrix}f(A)=K_{AB}\cdot x_{A}+b\\f(B)=K_{AB}\cdot x_{B}+b\end{matrix}\right.\)做差求得。
从图中不难看出,当两个点非常靠近时,AB直线的斜率就是切线斜率,我们将A点切线斜率定义为函数\(f(x)\)在A点导数值,记作\({f}’ (x_{A})\),则有:
$${f}’ (x_{A})=\lim_{x \to x_{A}} \frac{f(x)-f(x_{A})}{x-x_{A}}$$
\(\lim\)符号表示\(x\)自变量取值趋近于 \(x_{A}\)
例1:求\(f(x)=x^{2} 在x=1处的导数值\)
$$\begin{align*} {f}’ (1)&=\lim_{x \to 1} \frac{f(x)-f(1)}{x-1}\\ &=\lim_{x \to 1} \frac{x^{2} -1}{x-1}\\ &=\lim_{x \to 1} (x+1)\\&=2 \end{align*}$$
换句话说,也就是函数 \(f(x)=x^{2} \)在\(x=1\)处的的切线斜率为2,进一步可求出切线方程为\(y=2x-1\)
在导数定义如果令 \( x- x_{A} =\Delta x\) ,\(f(x_{A} +\Delta x)-f(x_{A} )=\Delta y\)则定义式可简化为:
$${f}’ (x_{A})=\lim_{ \Delta x \to 0 } \frac{\Delta y}{\Delta x}$$
上式为函数在某一点的导数;不难想到,对于函数的每一个点,都会有对应的导数值。因此自变量与导数值之间也构成了一个新函数,我们称之为导函数,可以定义为:
$${f}’ (x)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$$
使用\(\Delta y/\Delta x\)的写法可以体现出导数瞬时变化率也就是斜率的特点。
为了简便,上述定义式可以写为:
$${f}’ (x)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\frac{d y}{dx}$$
例2:求 \(f(x)=x^{3} 的导函数\)
$$\begin{align*} {f}’ (x)&=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}\\ &=\lim_{\Delta x \to 0} \frac{(x+\Delta x)^3-x^3}{\Delta x}\\ &=\lim_{\Delta x \to 0} \frac{x^3+3x^2\Delta x+3x\Delta x^2+\Delta x^3-x^3}{\Delta x}\\&=\lim_{\Delta x \to 0}\frac{3x^2\Delta x+3x\Delta x^2+\Delta x^3}{\Delta x}\\&=\lim_{\Delta x \to 0}3x^2+3x\Delta x+\Delta x^2\\&=3x^2 \end{align*}$$
左/右导数
在B点趋近A点的过程中,不光可以从右边趋近,还可以从左边趋近;也就是说对于趋近可以再细分为\(\lim_{x \to x_{A}^{+} }\)和\(\lim_{x \to x_{A}^{-} }\)两种情况:
例3:求\(a=\lim_{x \to 1^{-} }\frac{\left | x-1 \right | }{x-1} \)以及 \(b=\lim_{x \to 1^{+} }\frac{\left | x-1 \right | }{x-1} \)
$$\begin{align*} a&=\lim_{x \to 1^{-}} \frac{\left | x-1 \right | }{x-1}\\ &=\lim_{x \to 1^{-}} \frac{x-1}{x-1}\\ &=1 \end{align*}$$
$$\begin{align*} b&=\lim_{x \to 1^{+}} \frac{\left | x-1 \right | }{x-1}\\ &=\lim_{x \to 1^{+}} \frac{1-x}{x-1}\\ &=-1 \end{align*}$$
不难看出,上面的表达式是函数\(f(x)= \left | x-1 \right | \)分别在左边趋近1和右边趋近1时的导数值,而这个值是不同的。也就引出了如下定义:
左导数:
$${f}_{-}’ (x_{A})=\lim_{ \Delta x \to 0^- } \frac{f(x_{A} +\Delta x)-f(x_{A} )}{\Delta x}$$
a即为\(f(x)\)的左导数
右导数:
$${f}_{+}’ (x_{A})=\lim_{ \Delta x \to 0^+ } \frac{f(x_{A} +\Delta x)-f(x_{A} )}{\Delta x}$$
b即为\(f(x)\)的右导数
对于导数而言,无论是左趋近还是右趋近得到的导数值均应相同,也就是说如果一个函数有导数,那么导数=左导数=右导数
所以,对于函数\(f(x)= \left | x-1 \right | \),在\(x=1\)时左右导数不同, 因此它在\(x=1\)处没有导数,也就是没有切线。
导数的几何意义
根据导数的定义,如果一个函数在某点的导数大于0,那么有:
$$\begin{align*} f'(x)= \lim_{\Delta x \to 0} \frac{f(x+ \Delta x )-f(x)}{ \Delta x } >0 \end{align*}$$
- 如果\(\Delta x\)是右趋近于0,则\(\Delta x>0\),得到\(f(x+ \Delta x)>f(x)\),即\(x\)越大有\(f(x)\)越大,\(f(x)\)严格单调递增。
- 如果\(\Delta x\)是左趋近于0,则\(\Delta x<0\),得到\(f(x+ \Delta x)<f(x)\),即\(x\)越小有\(f(x)\)越小,\(f(x)\)严格单调递增。
综上所述,得到当某点的导数值大于0时,\(f(x)\)在此点附近严格单调递增。同理,如果某点的导函数小于0时,\(f(x)\)在此点附近严格单调递减。
导数作用
从上面的几何含义出发,如果导数\(f'(x)\)在\(x=a\)时取0,容易得到以下结论:
- 如果在\(x=a\)附近的左侧\(f'(x)<0\),右侧\(f‘(x)>0\),则\(a\)为\(f(x)\)的极小值点,\(f(a)\)为极小值。
- 如果在\(x=a\)附近的左侧\(f'(x)>0\),右侧\(f‘(x)<0\),则\(a\)为\(f(x)\)的极大值点,\(f(a)\)为极大值。
- 如果\(a\)既不是极大值点也不是极小值点,则称其为鞍点。
极大值点与极小值点统称为极值点,极大值与极小值统称为极值。极值不一定时最值,但是可以看成函数在\(x=a\)附近的最值点。
常见导数
根据之前导数的计算方法,可以计算出一些常见的导数公式:
$$(x^a)’=ax^{a-1}$$
$$(e^x)’=e^x$$
$$(ln x)’=\frac{1}{x}$$
$$(a^x)’=a^xln~a$$
$$(log_a~x)’=\frac{1}{xln~a}$$
$$(sin~x)’=cos~x$$
$$(cos~x)’=-sin~x$$
导数的运算
设\(u=u(x), v=v(x)\)都可导,则:
$$(u+v)’=u’+v’$$
$$(Cu)’=Cu’(C是常数)$$
$$(uv)’=u’v+v’u$$
$$(\frac{u}{v})’=\frac{u’v-uv’}{v^2}$$
偏导数
在现实生活中,一个因变量不一定只与一个自变量相关,因此引入多元函数,例如多元函数:
$$f(x,y)=x^2+y^2$$
对于这个函数,由于有两个变量,因此需要定义对不同变量的导数,称为偏导数,记作:
$$\frac{\partial{f}}{\partial{x}}、\frac{\partial{f}}{\partial{y}}$$
偏导数的定义如下:
$$\frac{\partial{f}}{\partial{x}}=\lim_{ \Delta x \to 0} \frac{f(x+\Delta x,y)-f(x,y )}{\Delta x}$$
$$\frac{\partial{f}}{\partial{y}}=\lim_{ \Delta y \to 0} \frac{f(x,y+\Delta y)-f(x,y )}{\Delta y}$$
对于上面函数,偏导数结果为:
$$\frac{\partial{f}}{\partial{x}}=2x、\frac{\partial{f}}{\partial{y}}=2y$$
对于多元函数,可以将不同方向的偏导数组合成一个向量,例如\((\frac{\partial{f}}{\partial{x}},\frac{\partial{f}}{\partial{y}})\)。我们称这个向量为梯度,根据导数的定义,函数沿着梯度方向变化最快,变化率最大。